Orienteering Distance Problem

About two weeks ago, my geometry class did their first project. I took the idea from Dan Schaben (Dan's blog), who I heard talk at Miama U’s (in Ohio) GeoGebra conference. The project is related to orienteering and involves angle measurements and a short distance to find the distance between two locations further away.

I was inspired by Dan’s project because I love the outdoors and the idea of using geometry to solve a practical problem. He also made the project local to his own school, and I wanted to do the same. It is my first year teaching in a new place and I wanted to connect to the students by making this project in a place they know. I spent a couple of days over the summer driving around and looking for locations I could use for the project. I needed two landmarks to find the distance between, but I soon realized that rural northwestern Indiana doesn’t have a lot of those. We have radio and cell phone towers, coops, and telephone lines. For this project I chose the local grain co-op and a tower of some sort (I can’t tell which are for phones or other things). Here are the videos I took. There are four of them because I don’t have / can’t find a simple video editor to combine them. I also tried to embed them but had difficulties, so you'll have to click on the link.

http://www.youtube.com/watch?v=4NmH37CZ8WA
http://www.youtube.com/watch?v=AwV6e8_eQ8Y
http://www.youtube.com/watch?v=10k1EFTmPqs
http://www.youtube.com/watch?v=N-h-ERwVfI0

Project Overview

This was the introduction to the project that I handed out to students:

Orienteering Distance Problem

In this problem, you are given headings on a compass for a radio tower and the Co-Alliance from two locations, as well as the distance and direction between the two locations. You will have to figure out from this information the distance between the radio tower and Co-Alliance.

You will be working in groups of 2-4. You may choose your own teammates, but think carefully about who you choose because part of your grade will be a group score for your work. Choose people who you work well with and who can help you succeed.

After you find a solution for this problem, we will review it as a class, and I will teach you how to construct the geometric solution using a program called GeoGebra.

After working through the first part of the problem, we will be taking a field trip to the parking lot where you will be taking your own measurements and compass headings to find the distance between two given landmarks. For this part of the problem, your group will be responsible for one drawing done in GeoGebra. Then each group member is individually responsible for a write-up on their solution. Your grade will consist of a combination of the group score and your individual score.

Good luck!

Leading up to this project, I had students practice estimating angles with the online game Kung Fu Angles. Another winner that we didn't have time to use is nrich's Estimating Angles. They didn’t get much time to play this game because of issues with laptops and logging on to the school network, and I would like for them to spend more time on it next year, but it was enough. Then I had them split up into their own groups of two to four, but recommended they choose good people to work with because part of their grade is based on a group score. From there, I showed them the video and had them start sketching solutions. Some groups got it quickly, and many had no idea what to do. I talked briefly about directions on a compass so that they knew 0° is North, 90° is East, 108° is South, and 270° is West. However I didn’t show them how to actually use a compass because I assumed that many of them would use a compass app on their cell phones later on in the project, and I only had 6 regular compasses to work with. At first I let students really struggle with the problem and the sketch. I didn’t give many hints, just let them play with it. We had a two-hour delay this day, so students didn’t get very long to work on their solutions.

The next day, I gave students ten more minutes to work on their sketches, then we reviewed the problem as a class. I did a sketch on the board and explained how to locate the two solutions with our sketch, and that GeoGebra would help us find the distance between them. After showing the solution on the board, I went on to show them how to construct the model on GeoGebra. Students have never seen GeoGebra and aren’t used to using computers in math class. I had a GeoGebra tool sheet from Jen Silver that shows where all the tools are, and I circled the ones we would be using, but not many students referred to it. Every student had a computer, and I stepped them through the construction of the model. The class was focused more on how GeoGebra works than on what the model means. In most of my Geometry classes we didn’t even get through the whole construction. Since many students didn’t log on to the computers, they couldn’t save their work, either. So I decided we would leave it at that – they wouldn’t have to finish these.

The next class was Tuesday after Labor Day, and we did two things: I walked them through the steps of the construction in GeoGebra, while they took notes. Then we went out to the parking lot for them to take their own measurements for the second part of the project. I wanted students to get a sense of why we had to take two angle measurements on the landmarks from two locations and why we had to measure the distance from our first location to our second location, as well as the direction. I wasn’t sure that they understood why they were working with that information when they were solving the problem from the videos. It makes more sense when you’re doing it in the field because you can see how the angle from you to a landmark changes as you move. I predetermined the landmarks and the locations where we would be taking the angles from because I wanted to be able to talk about the same landmarks when we had a group discussion. They would get different angle measurements on the two landmarks as it is, and I didn’t want to confuse things by having different landmarks as well.

While working outside, I suggested students use their phones because I didn’t have enough compasses for them all to use. Plus, the compasses are pretty crappy, and I would have to spend the time to teach them all how to use it. A couple of groups didn’t have a compass app between them, so I showed them how to use the handheld compass. They all took notes on the angles, as well as the distance between the two locations where they took the angle measures and the direction they walked. I think they enjoyed going outside, just to get out of the classroom and be with friends. It was a little chaotic because every group had to take the angle measurements from the same place. Since the distance we walked was only about 100 feet, they had to be pretty accurate about where they stood, or else their measurements would be off even more.

I gave the students the next day in class to create their own GeoGebra model in their groups. Some of them completed it, using the notes they had taken from my demonstration as well as what they remembered of doing it themselves at the beginning of the project. Since many were still not done, I gave them a little time in class the next day to complete it. If they were done, they could work on the write-up for the project. The rubric for that is below.

The project took a day longer than I expected, and I felt rushed even with that extra time. Many students were overwhelmed, confused, and frustrated. Most didn’t understand what they were doing, they just wanted to know how to do it and get it done. Some of those who figured it out didn’t know that they had it. I don’t know if the project was a success or failure.

See solutions and student work at the bottom of this post.

Reflections and Changes for Next Year

Looking back on the project, there are some changes I would make for next year. I forgot to have students estimate the distance between the co-op and the tower in the first part, and to estimate the distances of the landmarks outside in the second part. I need to show students how to use a compass and protractor before we start, even if they use their phone for a compass. When they used their phone, they often didn’t understand how or why it worked. I also need to know more about magnetic vs. true north because students had questions about it.

I considered doing the project without the first part – just having students take their own measurements outside. However, I think that doing the project twice – once with the videos and once with their own measurements – reinforced how it worked. I’m not sure many of them got it the first time.

I want to spend more time on the solution before we go the computers. I’ve also considered not using GeoGebra, and having them create the solution on graph paper. They would have to create a scale, and I could have them use the distance formula or Pythagorean Theorem, which they had just learned, to find the distance. I’m not sure the value of the using the computers is great enough. When students were first doing sketches of the problem in the video, when they got to finding the distance, they wanted to know how to do it. I said, that’s why we’re using the computers – using GeoGebra will make finding the distance really easy. One thing I skipped over is that the length of the line segment between the points for the two locations matters if you’re trying to find the distance between the locations on your sketch, but it doesn’t matter if your sketch is just a step in the process and you’re going to use a computer program to figure it out later.

I would like to do more modeling in the classroom. Once or twice when I was explaining the solution or talking about how the compass worked, I stood in one part of the classroom and took an “arm reading” to someone or something in the room. Then I moved 10 or so paces away and my arm stayed pointing at the person or object, but the angle changed as I moved. When we were working on the first part of the project with the videos, I had students imagine being at my first location (which happened to be a local gas station), and then driving further down the road – where were the co-op and the radio tower in reference to me at both locations? One of the advantages of doing the video in the local vicinity is that students had more information to work off of. They have their own knowledge of the locations and used that to help with their sketches. They could look at their paper and know where the co-op was in related to the road and the radio tower. When the showed it wrong on the paper and I corrected it, they realized they were wrong because of that knowledge, and the correction made practical sense to them because what we were talking about is in the real world.

I wish I had gotten students to do more of the talking, especially in sharing their sketches with each other. I didn’t like being the one in the front of the room explaining the solution and why it makes sense. That’s something I need to work on in general – facilitating student discussion and student presentation.

Throughout the project I sometimes changed names for things. I referred to their sketches and the GeoGebra model as a picture, a diagram, a drawing, a sketch, a construction, and finally a model. I settled on the word model, but should have used it from the start. I also needed names for the two locations where we took angles from, as well as the two landmarks, so I called them locations and landmarks respectively so students would know what I was talking about. Also, we had just finished learning how to bisect a line segment using a compass, and we would bisect an angle shortly after, and students were confused about the term compass – was it the thing we used for bisecting the segment, or was it the thing we used to measure angles and find North, South, East, and West? I still don’t know why the term is the same for both tools.

I would love for students to be able to justify the steps of the construction. For example, when you create the first ray off of the angle from the first location to the first landmark, that means that the landmark is located somewhere along that ray, we just don’t know where. The reason we have to get the second angle from a different location is because that will pinpoint the location of the landmark. That is why the intersection of the two rays locates the landmarks. You need the locations of the landmarks to find the distance between them for this project. I wonder if it would have helped to do a mini-project beforehand to help them get this. For example, I could have them locate something in the classroom, outside, or in the country based on two angle measurements for the object from two different locations. Then when we get to this project, they might better understand why we are using angle measurements and a distance to find another greater distance.

I asked students in class why the distance they got for both parts of the project was off from the actual distance (according to Google Earth), and many of them noted that the readings on the compass aren’t always accurate. I would like to add this question to their write-up.

During the project, I had one student who happens to live next to the tower I used in my video tell me that he had another solution. He wanted to use the Pythagorean Theorem (his work shown below) to determine the distance. Although the tower is not right on the road, and the two roads he wanted to use between the tower and the co-op do not meet at a perfect right angle, he got a decent solution. I was impressed that a student came up with an easier way, and actually went out and drove the distances. I didn’t give him time to share his solution with the class, which I intended to do, and I regret that. I think his solution is smart and I wish the rest of the students would have seen his idea and approach to the problem.

I would like to be more organized about the project next year, which I think is doable since now I’ve been through it once. I don’t think students knew exactly what was expected of them or what we were going to be doing every day. I’d like to give them a layout of the project and give them the grading rubric earlier on.

I was surprised how many students remembered how to do the GeoGebra construction a week later, even though they thought they forgot it. I know this because many students didn’t turn in the individual part of the project until a week later, and I had to get them started on writing the steps for the construction.

I would like to create a better assessment for the project as well. Like I said before, I would like for students to be able to justify the steps or explain why those are the steps that work. I’m not sure they really understand what they did or why it worked, and I don’t know how to assess it. I don’t know the question to ask. Many students said on survey forms that they were confused about the project. I don’t know how to make it clearer. Is it one of those things that just clicks or doesn’t? I’m glad we did the project twice – once with the measurements I took on the videos and once with their own measurements – because I think more students understood it the second time around. But I still think many don’t know what happened or why.

Finally, I wonder if the students understand the power of what we did. We used four angle measurements, a short distance, and a direction to figure out a much larger distance. If there was no way of measuring that large distance because maybe there are no roads between the two locations, this is a way to do it. Just like later on we will use a couple of measurements and trigonometry to find the height of something very tall. This is a powerful process in my opinion. I don’t know how to assess their understanding of this either.

Student Surveys

I had students fill out brief surveys at the end of the project to get some feedback. Here’s what it looked like (with spaces between the questions).

The responses that stood out to me are these: students were confused, they thought the project was boring, they liked going outside, some hated the computers or wanted to use CAD, and others liked using computers and GeoGebra, some wanted to learn how to use compasses, they wanted the compass measurements to be more accurate, some liked working in groups and some didn’t, they felt I should make the project and directions clearer or more organized or explain it better, they wanted to know how to do the project before we did it, they wanted it to be easier and not to have to write a paragraph on it, and they wanted more time to work on it or a later deadline.

Final Note

When I look back on the project, I hear the negative feedback more than the positive. I also wonder if any students got anything of value out of it. But I think about a project I had to do in my 10^th grade AP Statistics class. My teacher wanted us to analyze any game we wanted and explain the game using statistics. I chose tic-tac-toe, but I had no clue what he was looking for, and only vaguely understood what he was talking about. It was over my head. I think that's how some of my students feel about this project. But I still remember that project and how it challenged me to see mathematics differently. I only started to understand the meaning of the project in college. I think we need to stretch students and introduce them to things they don’t understand or think are posssible, whether they get it right then and there or not. I know it’s frustrating and hard to be confused, especially when you’re used to math class being straight forward, but I think that’s a task we as math teachers need to take on.


Notes
  
Here is what I consider to be student prerequisite knowledge for this project, though some of it I taught as I went:

Geometry

• 360 degrees in a circle
• What a vertex is
• Notation for angles with the vertex as the middle letter
• Angles
• Types of angles – acute, right, obtuse
• Vocab: points, lines, line segments, ray
• Intersection
• Perpendicular lines

Orienteering – perhaps do an example of using the compass in class

• How to use a compass 
• What a heading means on a compass 
• Degrees are clockwise from north 

GeoGebra Tools

• Point
• Line 
• Line segment 
• Ray 
• Angle of a given size 
• Intersecting two lines 
• Zoom 
• Dragging screen – panning 
• Putting away tools 
• Coloration and styling 
• Grid lines and axes 

Here are the steps to creating the model in GeoGebra:

• Create a line segment with a given distance
• Construct north-south line from first location.
• Find given angles for two towers and create rays for each one from the location point.
• Construct a north-south line from second location.
• Find given angles for two towers and create rays for each one from the location point.
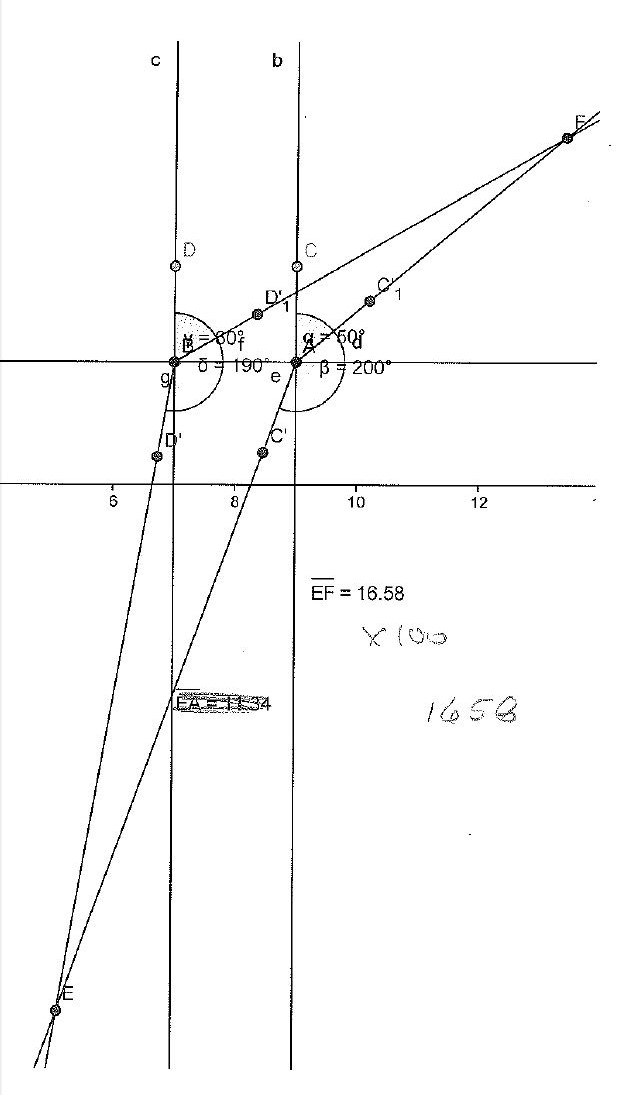
• Place a point at the intersection of the two headings for first landmark and a point at the intersection of the two headings for second landmark. The points are the locations of the landmarks.
• Find the distance between these two new points. That is the solution.

 

 

Solution to Video Problem (co-op to tower)

 

Solution to Student Problem (antenna to flag pole) and Student Work

 

First you have to go out and get the coordinates and angles for the problem. This is easy with a Iphone or good compass. Then go inside pull up the GeoGebra program. After you pull up the GeoGebra program, you have to make Point A and Point B. Put a line segment between the two. Then you have to make a perpendicular line that goes through Point B. Put Point C somewhere on that line. Then make angle of the required size from C to B. Make a ray through Point B at the angle that was created. Then do the same thing with Point D and A. After you do all of that do it again with the second set of degrees and angles. You should then have two points that are created by the intersecting rays. Measure the distance between the two points and you have your answer. That is how you find the distance between two points that you can't actually physically measure. It makes sense because it is the proven method that was probably used by ancient people and they could do amazing things with just some angles and compasses.